which just calls eval again!
When does it all end?

Eval calls apply,
which just calls eval again!
When does it all end?
In this project, you will develop an interpreter for a subset of the Scheme language. As you proceed, think about the issues that arise in the design of a programming language; many quirks of languages are the byproduct of implementation decisions in interpreters and compilers.
You will also implement some small programs in Scheme, including the
count_change function that we studied in lecture. Scheme is a simple but
powerful functional language. You should find that much of what you have learned about
Python transfers cleanly to Scheme as well as to other programming languages. To learn
more about Scheme, you can read the original Structure
and Interpretation of Computer Programs online for free. Examples from
chapters 1 and 2 are included as test cases for this project. Language
features from Chapters 3, 4, and 5 are not part of this project, but of
course you are welcome to extend your interpreter to implement more of the
language. Since we only include a subset of the language, your interpreter
will not match exactly the behavior of other interpreters such as STk.
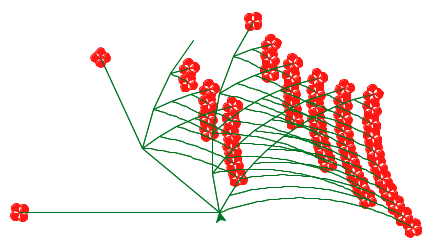
The project concludes with an open-ended graphics contest that challenges you to produce recursive images in only a few lines of Scheme. As an example of what you might create, the picture above abstractly depicts all the ways of making change for $0.50 using U.S. currency. All flowers appear at the end of a branch with length 50. Small angles in a branch indicate an additional coin, while large angles indicate a new currency denomination. In the contest, you too will have the chance to unleash your inner recursive artist.
This project includes several files, but all of your changes will be made to the
first three: scheme.py, scheme_reader.py, and
tests.scm. You can download all of the
project code as a zip archive.
scheme.py |
The Scheme evaluator |
scheme_reader.py |
The Scheme parser |
tests.scm |
A collection of test cases written in Scheme that are designed to test your Scheme interpreter. You will implement some Scheme procedures yourself. |
scheme_tokens.py |
A tokenizer for scheme |
scheme_primitives.py |
Primitive Scheme procedures |
scheme_test.py |
A testing framework for Scheme |
ucb.py |
Utility functions for 61A |
This is a two-part project. As in the previous project, you'll work in a team of two people, person A and person B. All questions are labeled sequentially, but some are designated for certain people by a prefix of their letter (A or B). Both partners should understand the solutions to all questions.
In the first part, you will develop the interpreter in stages:
In the second part, you will implement Scheme procedures that are similar to some exercises that you previously completed in Python.
There are 27 possible correctness points and 3 composition points. The composition score in this project will evaluate the clarity of your code and your ability to write tests that verify the behavior of your interpreter.
When you are done, submit the project using submit proj4. The
only files you are required to submit
are scheme.py, scheme_reader.py,
and tests.scm.
Before you begin working on the project, review what you have learned in lecture about the Scheme language in Chapter 3.5 of the course lecture notes.
Read-Eval-Print. Run interactively, the interpreter reads Scheme
expressions, evaluates them, and prints the results. The interpreter uses
scm> as the prompt.
scm> 2
2
scm> (((lambda (f) (lambda (x) (f f x)))
(lambda (f k) (if (zero? k) 1 (* k (f f (- k 1)))))) 5)
120
The starter code for your Scheme interpreter in scheme.py
can successfully evaluate the first expression above, since it consists of a
single literal numeral. The second (a computation of 5 factorial) will not
work just yet.
Load. Our load function differs from standard Scheme
in that we use a symbol for the file name. For example,
scm> (load 'tests)
Symbols. Unlike some implementations of Scheme, in this project numbers and boolean values cannot be used as symbols. Symbols may not be capitalized.
Turtle Graphics. In addition to standard Scheme procedures, we
include procedure calls to the Python turtle package. Read its
documentation.
Note: The turtle Python module may not
be installed by default on your personal computer. However, the
turtle module is installed on the instructional machines.
So, if you wish to create turtle graphics for this project (i.e. for
the contest), then you'll either need to setup turtle on
your personal computer, or test on your class account.
The tests for this project are largely taken from the Scheme
textbook that 61A used for many years. Examples from relevant
chapters (and a few more examples to test various corner cases)
appear in tests.scm.
You can also compare the output of your interpreter to the expected output
by running scheme_test.py.
python3 scheme_test.py
The tests.scm file contains Scheme
expressions interspersed with comments in the form:
(+ 1 2)
; expect 3
(/ 1 0)
; expect Error
Above, scheme_test.py will evaluate (+ 1 2)
using your code in scheme.py, then output a test failure
if 3 is not returned. The second example tests for an error
(but not the specific error message). The scheme_test script
collects these expected outputs and compares them with the actual output from
the program, counting and reporting mismatches.
Only a small subset of tests are designated to run by default because
tests.scm contains an (exit) call near the
beginning, which halts testing. As you complete more of the project, you
should move or remove this call. Note that your interpreter doesn't know
how to exit until Problems 3 and 4 are completed.
Important: As you proceed in the project, add new tests to the top
of tests.scm to verify the behavior of your implementation.
Finally, as always, you can run the doctests for the project using:
python3 -m doctest scheme.py scheme_reader.py
Don't forget to use the trace decorator from the
ucb module to follow the path of execution in your
interpreter.
As you develop your Scheme interpreter, you may find that Python raises
various uncaught exceptions when evaluating Scheme expressions. As a result,
your Scheme interpreter will crash. Some of these may be the results of bugs
in your program, and some may be useful indications of errors in user
programs. The former should be fixed (of course!) and the latter should be
caught and changed into SchemeError exceptions, which are caught
and printed as error messages by the Scheme read-eval-print loop we've
written for you. Python exceptions that "leak out" to the user in raw form
are errors in your interpreter (tracebacks are for implementors, not
civilians).
To run your Scheme interpreter in an interactive mode, type:
python3 scheme.py
Alternately, you can tell your Scheme interpreter to evaluate the
lines of an input file by passing the file name as an argument to
scheme.py:
python3 scheme.py tests.scm
Currently, your Scheme interpreter can handle a few simple expressions, such
as:
scm> 1
1
scm> 42
42
scm> #t
True
To exit the Scheme interpreter, issue either Ctrl-c or
Ctrl-d or evaluate the exit procedure:
scm> (exit)
The function scheme_read in scheme_reader.py
parses a Buffer (buffer.py) instance that returns
valid Scheme tokens on invocations of current and
pop methods. It returns the next full Scheme expression in the
src buffer, using an internal representation as follows:
| Scheme Data Type | Our Internal Representation |
|---|---|
| Numbers | Python's built-in int and float data types.
|
| Symbols | Python's built-in string data type. |
Booleans (#t, #f) |
Python's built-in True, False
values. |
| Pairs | The Pair class, defined in the
scheme_reader.py file. |
| nil | The nil object, defined in the
scheme_reader.py file. |
Problem 1 (1 pt). Complete the scheme_read function in
scheme_reader.py by adding support for quotation.
src is the string
"nil", return the nil object. (provided)
'bagel), then treat the quoted symbol as the special form
(quote bagel).
"(", return
the result of read_tail. (provided)
Problem 2 (2 pt). Complete the read_tail function in
scheme_reader.py by adding support for dotted lists. A dotted
list in Scheme is not necessarily a well-formed list, but instead has an
arbitrary second attribute that may be any Scheme value.
The read_tail function expects to read the rest of a list or
dotted list, assuming the open parenthesis has already been popped by
scheme_read.
Consider the case of calling scheme_read on input "(1 2
. 3)". The read_tail function will be called on the
suffix "1 2 . 3)", which is
1 and the value of the tail
"2 . 3)", which is
2 and the Scheme value
3.read_tail would return Pair(1, Pair(2, 3)).
Hint: In order to verify that only one element follows a dot, after
encountering a '.', read one additional expression and then
check to see that a closing parenthesis follows.
To verify that your solutions to Problem 1 and 2 work correctly, run the
doctests for scheme_reader.py and test your parser interactively
by running,
# python3 scheme_reader.py
read> 42
42
read> '(1 2 3)
(quote (1 2 3))
read> nil
()
read> '()
(quote ())
read> (1 (2 3) (4 (5)))
(1 (2 3) (4 (5)))
read> (1 (9 8) . 7)
(1 (9 8) . 7)
read> (hi there . (cs . (student)))
(hi there cs student)
All further changes to the interpreter will be made in
scheme.py. For each question, add a few tests to the top of
tests.scm to verify the behavior of your implementation.
Chapter
3.7 of the course lecture notes describes the structure of the Scheme
evaluator. In the implementation given to you, the scheme_eval
function is complete, but few of the functions or methods it uses are
implemented. In fact, the evaluator can only evaluate self-evaluating
expressions: numbers, booleans, and nil.
Problem 3 (2 pt). Implement apply_primitive, which is
called by scheme_apply for PrimitiveProcedures.
Primitive procedures are applied by calling a corresponding Python function
that implements the procedure.
Scheme primitive procedures are represented as instances of the
PrimitiveProcedure class, defined in
scheme_primitives.py. A PrimitiveProcedure has two
instance attributes:
self.fn is the self.use_env is a boolean flag that indicates whether or
not this primitive procedure will expect the current environment to be
passed in as the last argument. The environment is required, for instance,
to implement the primitive eval procedure.To see a list of all Scheme primitive procedures used in the project, look
in the scheme_primitives.py file. Any function decorated with
@primitive will be added to the globally-defined
_PRIMITIVES list.
The apply_primitive function takes a
PrimitiveProcedure instance, a Scheme list of argument values,
and the current environment. Your implementation should:
procedure.use_env is True, then
add the current environment env as the last argument.
procedure.fn on those arguments (hint: use *
notation).
TypeError exception
being thrown, then raise a SchemeError instead.The doctest for apply_primitive should now pass. However,
your Scheme interpreter will still not be able to apply primitive
procedures, because your Scheme interpreter still doesn't know
how to look up the values for the primitive procedure symbols (such as
+, *, and car).
Problem 4 (2 pt) Implement the lookup method of the
Frame class. It takes a symbol (Python string) and returns the
value bound to that name in the first frame of the environment in which it is
found. A Frame represents an environment via two instance
attributes:
self.bindings is a dictionary that maps Scheme symbols
(represented as Python strings) to Scheme values.
self.parent is the parent Frame
instance. The parent of the Global Frame is None.
lookup implementation should,
self.bindings if it exists.
lookup that symbol in the parent if it exists.
SchemeError.
After you complete this problem, you should be able to evaluate primitive procedure calls, giving you the functionality of the Calculator language and more.
scm> +
#[primitive]
scm> (+ 1 2)
3
scm> (* 3 4 (- 5 2) 1)
36
scm> (odd? 31)
True
Problem A5 (1 pt). There are two missing parts in the method
do_define_form, which handles the (define ...)
special forms. Implement just the first part, which binds names to values
but does not create new procedures. do_define_form should return
the name after performing the binding.
scm> (define tau (* 2 3.1415926))
tau
You should now be able to give names to values and evaluate symbols to those values.
scm> (define x 15)
x
scm> (define y (* 2 x))
y
scm> y
30
scm> (+ y (* y 2) 1)
91
scm> (define x 20)
x
scm> x
20
Problem B6 (1 pt). Implement the do_quote_form
function, which evaluates the quote special form. Once you have
done so, you can evaluate quoted expressions.
scm> 'hello
hello
scm> '(1 . 2)
(1 . 2)
scm> '(1 (2 three . (4 . 5)))
(1 (2 three 4 . 5))
scm> (car '(a b))
a
scm> (eval (cons 'car '('(1 2))))
1
At this point in the project, your Scheme interpreter should be be able to support the following features:
quote special form,(+ (- 4 2) 5) In our interpreter, user-defined procedures will
be represented as instances of the LambdaProcedure class,
defined in scheme.py. A LambdaProcedure
instance has three instance attributes:
self.formals is a Scheme list of the formal
parameters (symbols) that name the arguments of the procedure.
self.body is a single Scheme expression; the body of the
procedure.
self.env is the environment in which the procedure was
defined. Problem 7 (2 pt). Implement the begin special form,
which has a list of one or more sub-expressions that are each evaluated in
order. The value of the final sub-expression is the value of the
begin expression.
scm> (begin (+ 2 3) (+ 5 6))
11
scm> (begin (display 3) (newline) (+ 2 3))
3
5
Note: When scheme_eval evaluates one of
the conditional constructs (if, and,
or, cond, begin,
case), notice that it calls scheme_eval
on the return value of the relevant do_FORM
procedures (do_begin_form, do_cond_form, etc.).
Take care that your Scheme interpreter doesn't inadvertantly call
scheme_eval on the same value twice, or else you might
get the following invalid behavior:
scm> (begin 30 'hello)
Error: unknown identifier: hello
Problem 8 (2 pt). Implement the do_lambda_form method,
which creates LambdaProcedure values by evaluating
lambda expressions. While you cannot call a user-defined
procedure yet, you can verify that you have read the procedure correctly by
evaluating a lambda expression.
scm> (lambda (x y) (+ x y))
(lambda (x y) (+ x y))
In Scheme, it is legal to have function bodies with more than one expression:
STk> ((lambda (y) 42 (* y 2)) 5)
10
In order to implement this feature, your
do_lambda_form should detect when the body of a lambda
expression contains multiple expressions. If so, then
do_lambda_form should place the expressions
inside of a (begin ...) expression, and use that
begin expression as the body:
scm> (lambda (y) 42 (* y 2))
(lambda (y) (begin 42 (* y 2)))
Problem A9 (1 pt). Currently, your Scheme interpreter is able to define user-defined procedures in the following manner:
scm> (define f (lambda (x) (* x 2)))
f
However, we'd like to be able to use the shorthand form of defining
procedures:
scm> (define (f x) (* x 2))
f
Modify the do_define_form function so that it correctly
handles the shorthand procedure definition form above. Make sure that it can
handle multi-expression bodies. Hint: construct a lambda
expression and evaluate it with do_lambda_form.
Once you have completed this problem, you should find that defined procedures evaluate to lambda procedures.
scm> (define (square x) (* x x))
square
scm> square
(lambda (x) (* x x))
Problem 10 (2 pt). Implement the make_call_frame method of
the Frame class. It should do 2 things:
self (done for you).
Make sure the number of arguments make_call_frame recieves is the same as the number of formal parameters it recieves.
Problem B11 (1 pt). Implement the check_formals
function to raise an error whenever the Scheme list of formal parameters
passed to it is invalid. Raise a SchemeError if the list of
formals is not a well-formed list of symbols or if any symbol is
repeated. (Hint: Look inside of scheme_primitives.py for a function that tells you something is a scheme symbol. )
Problem 12 (2 pt). Implement scheme_apply to correctly
apply user-defined LambdaProcedure instances. (The case of
MuProcedures is handled later in the project). It should:
Frame, with all formal parameters
bound to their argument values.
procedure in the environment
represented by this new frame.
procedure.
After you complete scheme_apply, user-defined functions (and
lambda functions) should work in your Scheme interpreter. Now is an
excellent time to revisit the tests in tests.scm and ensure that
you pass the ones that involve definition (Sections 1.1.2 and 1.1.4). You
should also add additional tests of your own to verify that your interpreter
is behaving as you expect.
The basic Scheme logical special forms are if,
and, or, and cond. These expressions
are special because not all of their sub-expressions may be evaluated.
In Scheme, only #f (also known as false or
False) is a false value. All other values are true values. You
can test whether a value is a true value or a false value using the provided
Python functions scheme_true and scheme_false,
defined in scheme_primitives.py.
Problem A13 (1 pt). Implement do_if_form so that
if expressions are evaluated correctly. This function should
return either the second (consequent) or third (alternative) expression of
the if expression, depending on the value of the first
(predicate) expression.
scm> (if (= 4 2) true false)
False
scm> (if (= 4 4) (* 1 2) (+ 3 4))
2
It is legal to pass in just two expressions to the if special
form. In this case, you should return the second expression if the first
expression evaluates to a true value. Otherwise, return the special
okay value, which represents an undefined value.
scm> (if (= 4 2) true)
okay
Problem B14 (2 pt). Implement do_and_form and
do_or_form so that and and or
expressions are evaluated correctly.
The logical forms and and or are short-
circuiting. For and, your interpreter should evaluate each
sub-expression from left to right, and if any of these evaluates to
False, then False is returned. If all but the last
sub-expressions evaluate to true values, return the last sub-expression from
do_and_form.
For or, evaluate each sub-expression from left to right. If any
evaluates to a true value, then quote that value and return it.
These return values must be quoted because they are evaluated in
scheme_eval. If all but the last sub-expression evaluate to
false, return the last sub-expression from do_or_form without
quoting it.
scm> (and)
True
scm> (or)
False
scm> (and 4 5 6)
6 ; all operands are true values
scm> (or 5 2 1)
5 ; 5 is a true value
scm> (and #t #f 42 (/ 1 0))
False ; short-circuiting behavior of and
scm> (or 4 #t (/ 1 0))
4 ; short-circuiting behavior of or
Problem A15 (1 pt). Implement do_cond_form so that it
returns the first result sub-expression corresponding to a true predicate (or
else). Your implementation should match the following examples and the
additional tests in tests.scm.
scm> (cond ((= 4 3) 'nope)
((= 4 4) 'hi)
(else 'wait))
hi
scm> (cond ((= 4 3) 'wat)
((= 4 4))
(else 'hm))
True
scm> (cond ((= 4 4) 'here 42)
(else 'wat 0))
42
For the last example, where the body of a cond case has multiple
expressions, you might find it helpful to replace
cond-bodies with multiple expression bodies into a
single begin expression, i.e., the following two expressions are
equivalent.
(cond ((= 4 4) 'here 42))
(cond ((= 4 4) (begin 'here 42)))
If the body of a cond case is empty,
then do_cond_form should quote the value of the predicate and
return it, if the predicate evaluates to a true value.
scm> (cond (12))
12
scm> (cond ((= 4 3))
('hi))
hi
The value of a cond is undefined if there are no true
predicates and no else. In such a case, do_cond_form
should return okay.
Problem A16 (2 pt). The let special form introduces local
variables, giving them their initial values. For example,
scm> (define x 'hi)
x
scm> (define y 'bye)
y
scm> (let ((x 42)
(y (* 5 10)))
(list x y))
(42 50)
scm> (list x y)
(hi bye)
Implement
the do_let_form method to have this effect and test it, by
adding test cases to tests.scm. Make sure your let
correctly handles multi-expression bodies:
scm> (let ((x 42)) x 1 2)
2
The let special form is equivalent to creating and then calling a lambda procedure. That is, the following two expressions are equivalent:
(let ((x 42) (y 16)) (+ x y))
((lambda (x y) (+ x y)) 42 16)
Thus, a let form implicitly creates a new
Frame (containing the let bindings)
which extends the current environment and evaluates the body of the
let with respect to this new Frame. This is
very much exactly like a user-defined function call. Note that, in your
project code, you don't have to actually create a
LambdaProcedure and call it. Instead, you can
create a new Frame, add the necessary bindings, and
evaluate the expressions of the let body with respect to
the new Frame.
The bindings created by a let are not able to refer back to
previously-declared bindings from the same let.
Problem B17 (2 pt). Implement do_mu_form to evaluate
the mu special form, a non-standard Scheme expression type. A
mu expression is similar to a lambda expression,
but evaluates to a MuProcedure instance that is dynamically
scoped. The MuProcedure class has been provided for you.
Additionally, complete scheme_apply to call
MuProcedure procedures using dynamic scoping. Calling a
LambdaProcedure uses lexical scoping: the parent of the new call
frame is the environment in which the procedure was defined. Calling a
MuProcedure created by a mu expression uses dynamic
scoping: the parent of the new call frame is the environment in which the
call expression was evaluated. As a result, a MuProcedure does
not need to store an environment as an instance attribute. It can refer to
names in the environment from which it was called.
scm> (define f (mu (x) (+ x y)))
f
scm> (define g (lambda (x y) (f (+ x x))))
g
scm> (g 3 7)
13
Your Scheme interpreter implementation is now complete. You should have
been adding tests to tests.scm as you did each problem. These
tests will be evaluated as part of your composition score for the project.
Make sure that your project works as expected.
Not only is your Scheme interpreter itself a tree-recursive program, but it is
flexible enough to evaluate other recursive programs. Implement the following
procedures in Scheme at the bottom of tests.scm.
Problem 18 (2 pt). Implement the merge procedure, which
takes in a comparator and two sorted list arguments and combines them into one
sorted list. A
scm> (merge < '(1 4 6) '(2 5 8))
(1 2 4 5 6 8)
scm> (merge > '(6 4 1) '(8 5 2))
(8 6 5 4 2 1)
Problem A19 (2 pt). Implement the count-change procedure, which
counts all of the ways to make change for a total amount, using coins with
various denominations (denoms), but never uses more than
max-coins in total. The procedure definition line is provided
in tests.scm, along with a list of U.S. denominations.
Problem B20 (2 pt) Implement the count-partitions procedure,
which counts all the ways to partition a positive integer total using only
pieces less than or equal to another positive integer max-value. The
number 5 has 5 partitions using pieces up to a max-value of
3:
3, 2 (two pieces)
3, 1, 1 (three pieces)
2, 2, 1 (three pieces)
2, 1, 1, 1 (four pieces)
1, 1, 1, 1, 1 (five pieces)
Problem 21 (2 pt). Implement the list-partitions procedure,
which lists all of the ways to partition a positive integer total into at
most max-pieces pieces that are all less than or equal to a positive
integer max-value. Hint: Define a helper function to construct
partitions.
Problem 22 (0 pt). Implement the hax procedure that
draws the following recursive illustration when passed two arguments, a side
length d and recursive depth k. The example below
is drawn from (hax 200 4).
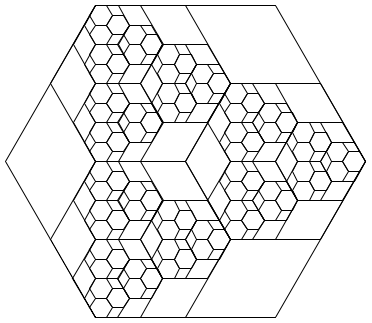
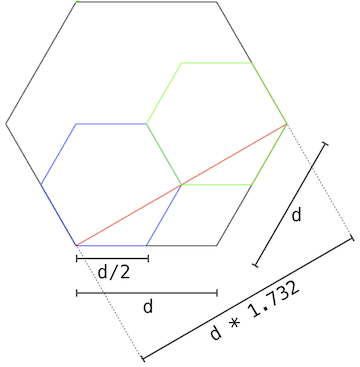
To see how this illustration is constructed, consider this annotated version that gives the relative lengths of lines of the component shapes in the figure.
Problem 23 (2 pt). Complete the function
scheme_optimized_eval
in scheme.py. This alternative to scheme_eval is
properly tail recursive. That is, the interpreter will allow an unbounded
number of active tail
calls in constant space.
Instead of recursively calling scheme_eval for tail calls and
logical special forms, and let, replace the current
expr and env with different expressions and
environments. For call expressions, this change only applies to calling
user-defined procedures.
Once you finish, uncomment the line
scheme_eval = scheme_optimized_eval in scheme.py.
Congratulations! You have finished the final project for 61A! Assuming your tests are good and you've passed them all, consider yourself a proper computer scientist!
Now, get some sleep. You've earned it!
We've added a number of primitive drawing procedures that are collectively
called "turtle graphics". The turtle represents the state of the drawing
module, which has a position, an orientation, a pen state (up or down), and a
pen color. The tscheme_x functions in
scheme_primitives.py are the implementations of these
procedures, and show their parameters with a brief description of each.
The Python documentation of
the turtle module contains more detail.
Contest. Create a visualization of an iterative or recursive process
of your choosing, using turtle graphics. Your implementation must be written
entirely in Scheme using the interpreter you have built. However, you may add
primitive procedures to interface with Python's turtle
or math modules. Other than that
all computation must be done in Scheme. If you do add new primitives,
then make sure to submit scheme_primitives.py in addition
to contest.scm.
Prizes will be awarded for the winning entry in each of the following categories, as well as 3 extra credit points.
Entries (code and results) will be posted online, and winners will be selected by popular vote as part of a future homework. The voting instructions will read:
Please vote for your favorite entry in this semester's 61A Recursion Exposition contest. The winner should exemplify the principles of elegance, beauty, and abstraction that are prized in the Berkeley computer science curriculum. As an academic community, we should strive to recognize and reward merit and achievement (translation: please don't just vote for your friends).
To improve your chance of success, you are welcome to include a title and descriptive haiku in the comments of your entry, which will be included in the voting.
Entries that do not construct an image iteratively or recursively may be disqualified. This includes just drawing a preexisting image, even if the drawing function is iterative or recursive.
Submission instructions will be posted shortly.
We have implemented a significant subset of Scheme in this project, but our interpreter can be extended with more features. Some suggestions can be found here.